4 min read
The Fundamentals of Oil & Gas Hedging - Put Options
This post is the third in a series where we are exploring how oil and gas producers can hedge their exposure to crude oil, natural gas and NGL...
5 min read
Mercatus Energy : May 31,2019

In our last post, Can Activity in Crude Oil Options Provide Insight into Crude Oil Price Trends, we explored the definition of delta, as well as it’s little brother, gamma:
Delta: the rate at which an option’s premium changes for a given change in the underlying
Gamma: the rate at which an option’s delta change for a given change in the underlying.
There is so much information contained in these two calculations, that we thought it would be useful to revisit the deep out-of-the-money (OTM) call options from last week to more deeply explore delta and gamma. As we noted last week, deep OTM calls can be used to offset the risk contained in a portfolio of short swaps. For example, assume an exploration and production company (E&P) sold a December 2019 swap at $60 on 28 November 2018 to hedge expected production. This established a $60 fixed price, below which E&P has mark-to-market (MtM) gains and above which E&P suffers MtM losses.
In this scenario, the potential for MtM losses on the hedge is considered “right way risk.” E&P’s various financial counterparties, such as their lenders, see these hedging losses as reasonable because as the price of oil increases, the revenue generating capability of E&P increases, offsetting the hedge losses. Hedging losses in this sense are opportunity costs, assuming they aren’t so large that they affect the financial well being of the company. Still, the “risk manager” at E&P, often the CFO or treasurer, may not be comfortable with this trade off.
Purchasing a deep OTM call is one way to reduce the potential impact of MtM losses on the swap. The $100 call doesn’t completely offset the potential MtM loss because it is so far OTM from $60, but the premium outlay is significantly lower than an option that is near the money. Using the delta and the gamma, we can look back and see how the combination of a long $100 Brent call and short $60 swap would have performed as a hedge over the last six months and see how the call acts as insurance against rising oil prices and impacts the net-hedged position of the E&P company.
| E&P Swap + Deep OTM Call | Barrels | Premium | Delta | Gamma |
| Sell Brent Swap | 1,000 | n/a | -1.00 | n/a |
| Buy Brent Call Option | 1,000 | $0.20/BBL | 0.035 | 0.045 |
Notice that the swap has a negative delta and no gamma. Intuitively, the swap must change at 100% the rate of the underlying value of oil. This delta is fixed and negative because it is a short contract. A fixed delta has no rate of change, so a gamma of 0. The call position has a small, but positive delta. Long calls always have positive delta. The net delta of the position is calculated as follows:
(1,000 BBLs swaps x -1.00 delta) + (1,000 BBLs call options x 0.35 delta) = -965 net delta
Textbook references to delta hedging are usually different than how we’ll describe it here. Delta hedging is commonly described from the perspective of the options trader, not the corporate risk manager. As an options trader, who utilizes options as a speculative tool, one may want to be delta neutral. In other words, an options trader my want to eliminate the potential impact the changing value of the underlying swap has on his or her options position. In this way, the options trader uses the delta to determine the hedge ratio. The delta neutral position, or a hedge ratio of zero, is calculated by dividing 1 by the options position’s net delta. For example, if the trader’s portfolio was long, 10 at-the-money call options with a delta of 0.50, he or she would need a ratio of 2 long calls to 1 contract short in the underlying swap to delta hedge his speculative position:
(10 x 0.50) call options + (-5 x 1) short swaps = 0 net delta
An E&P company who has hedged with a short $60 swap isn’t interested in reaching delta neutrality. In fact, the company wants the benefits of the swap if prices fall below $60. It is unlikely that the risk manager would purchase the roughly 29:1 (1.00/0.035) ratio of calls to swaps necessary to reach delta neutrality. This would likely be cost prohibitive, given the stated desire to minimize premium. Besides, the E&P’s physical assets provide the benefit of offsetting MtM hedging losses with rising revenues, as described above. So how do we interpret this hedge ratio in a way that is useful to the E&P?
In this case, the hedge ratio might be better expressed as a percentage of the E&P’s production volume. For example, if the company expects to produce 1,000 bbls of oil next December, the net delta position of –965 translates into a 96.5% hedge as of the day it was established. This hedged position shifts according to the delta and gamma as the price of oil changes. E&P slowly recovers the opportunity lost on the $60 short swap as the call gains value when oil prices increase. It isn’t a perfect match, but it reduces the hedged position proportionate to the rate at which delta rises, reducing the net percentage of volume hedged, and possibly allowing the company to establish additional short hedges at higher prices without over hedging.
Using our hypothetical position and market data from 29 November 2018 through 28 May 2019, we can see how this ratio changed.
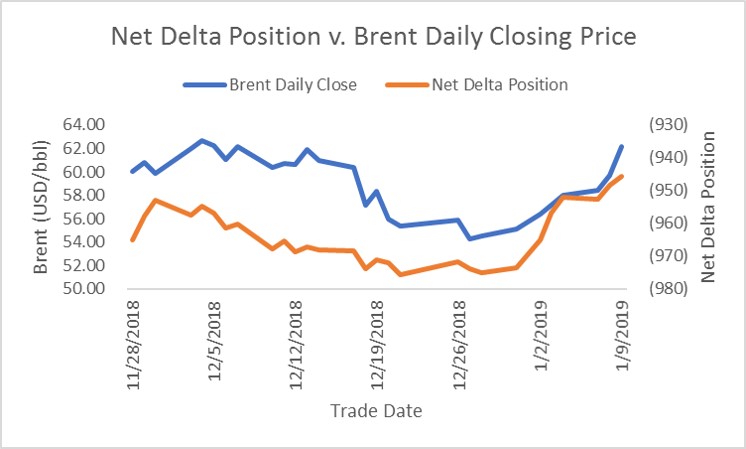
Notice how the orange line, which represents the net delta position, moves with the blue line depicting the price of crude oil. As prices fell from $60.06 to $55.35 during December, the net position got shorter, dropping from –965 to –976 net delta. This is because the delta of the $100 call position fell from 35 to 24. On the other hand, as prices rebounded from that late-December low of $55.35, the net delta position rose, peaking at –946 on 9 January 2019. Still short, representing an appropriate hedge, but reducing the net position to reflect the long call’s changing value.
The delta position changed at the rate defined by gamma. In our example, gamma started at 4.5. All long options have positive gamma. For the long all, this means the delta gets larger as the price of the underlying rises. As oil prices rise toward the $100 strike price, the delta will rise from 0.035, accelerating the rate at which the premium rises relative to the underlying and further reducing our net-hedged ratio. From 28 November 2018 to 9 January 2019, as Brent prices fell then rebounded, the gamma fell from 4.5 to 3.66, then rose to 6.42, showing how the rate at which delta changed as the call moved deeper out of the money and back. Delta falls toward zero as the call falls further out of the money. This means the net-hedged position in our example moves toward –1,000, or fully hedged for E&P. The inverse is also true as the price of oil rises and the call option moves toward being in the money and delta approaches 1.00, which would offset the MtM loss on the swap proportionately for every $1 oil rose after that point.
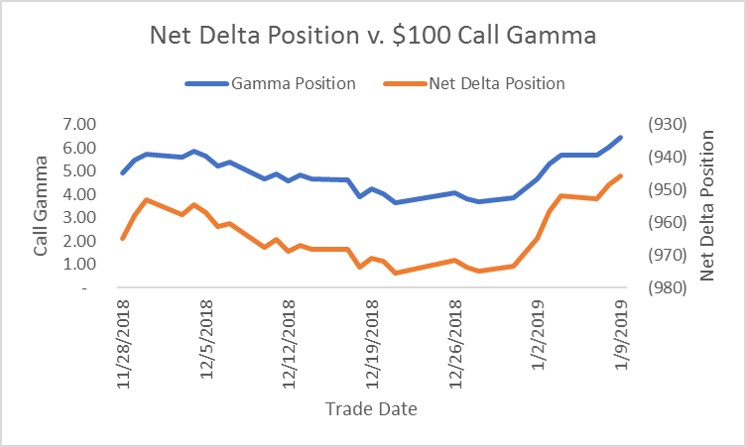
The “art” skills required of someone tasked with hedging a oil and gas producer, or consumer, is to determine the appropriate balance of premium and delta/gamma for your particular risk tolerance and corporate goals. In this example, the risk manager chose to spend $0.20/bbl, about $200 on the position, to purchase insurance against MtM losses on a $60 swap position. The premium was low relative to the notional value of the position. $200 is about 0.3% of the $60,000 original notional value of the swap position. The premium fell from $0.20 on 28 November 2018 to approximately $0.135 at its lowest, before rising to $0.36 on 9 January 2019. As an option buyer, the risk manager was not subject to MtM losses, but as the option’s value rose, he had the right to capture the benefit by selling the option. Brent peaked on 9 January 2019 at $62.15/bbl. At this point the call MtM gain $0.16/bbl, or about $160 on the 1,000 bbl position. At $62.15, the swap was $2.15 underwater, which is about $2,150 on the 1,000 bbl position. The deep OTM call reduced the MtM loss by about 7.4%.
This is exactly what the E&P company wants in our hypothetical demonstration. The risk manager created a portfolio that protects the company from falling prices, while maintaining affordable insurance against a drastic rise in prices, always hedged at the net delta position.
One last thing – we didn’t cover it here, but this also impacts E&P’s credit position. If the hedging counterparty has extended credit to E&P or if E&P has to manage margin requirements in a clearing account, the portfolio is analyzed on a net basis. As a result, combining a short swap with a long call, even deep OTM, reduces the credit risk associated with E&Ps hedges, when compared to a hedge consisting of only short swaps.

4 min read
This post is the third in a series where we are exploring how oil and gas producers can hedge their exposure to crude oil, natural gas and NGL...
2 min read
As we discussed A Beginner's Guide to Crude Oil Options - Part I & Part II, there are four primary factors that determine the price of crude oil, as...

4 min read
Unprecedented price decline presents hedge optimization opportunities As a result of the significant decline in crude oil prices, E&P companies who...